ضرب سریع اعداد در 9

مرحله1:عدد را در 10 ضرب کرده

مرحله2:عدد بدست آمده از مرحله قبل را منهای خودش(عددی که در 9 ضرب شده است)می کنیم

مرحله3:جواب بدست آمده

                         مرحله3           مرحله 2             مرحله 1

15×9=             15×10                  150-15             135

68×9=             68×10                  680-68              612

654×9=           654×10               6540-654           5886

محاسبه جذر اعداد با فرجه دلخواه

 

_{در این بحث روش محاسبه جذر اعداد با فرجه دلخواه را برای شما قرار داده ایم . برای مشاهده روش محاسبه بر روی ادامه مطلب کلیک کنید.}

_{با استفاده از این روش می توانید جذر اعداد را با فرجه دلخواه محاسبه نمایید . این روش دارای حد اکثر پنج صدم خطا می باشد و روش مناسبی برای جذر گیری است. با استفاده از فرمول
زیر می تواند حاصل جذر را به صورت یک کسر به دست آورده و در صورت تمایل با تقسیم صورت بر مخرج حاصل را به طور تقریبی بیابید. فرمول کلی به شکل زیر است.}

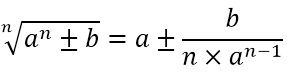
_{مثال: حاصل جذر را های زیر را بیابید.}

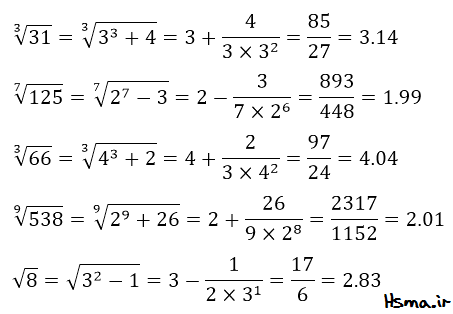
_{نکته: هر چه عدد مورد نظر بزرگ تر باشد خطا جذر گیری با استفاده ز این روش کمتر می باشد.}

اتـــــــــــــــــــــحادهــــــــــــــــــا ریاضی نهم

آموزش اتحادها

آموزش تجزیه عبارت ها کلاس هشتم و نهم

دانلود مقاله تجزیه عبارت های جبری

نکته هایی در مورد چند ضلعی ها

تعریف چند ضلعی :
هر خط شکسته بسته را چند ضلعی می نامند . مثلث یک چند ضلعی (سه ضلعی) است. اگر یکی از زوایای داخلی چند ضلعی بزرگتراز 180 درجه باشد،چند ضلعی را مقعر و در غیر این صورت چند ضلعی را محدب می نامند.

نکته 1 :
مجموع اندازه های زوایای هر n ضلعی برابر  180*(2-n )درجه است.
برای مثال ، مجموع اندازه های زوایای یک هفت ضلعی برابر با 900درجه است.

نکته 2 :
تعداد قطرهای هر n ضلعی محدب برابر با

½ (n)(n-3)

است.

نکته 3 :
در چند ضلعیهای منتظم با تعداداضلاع زوج، اضلاع مقابل بر هم ، با هم موازیند.
نکته 4 :
در هر چند ضلعی منتظم با تعداد اضلاع فرد، عمودمنصف هر ضلع ، نیمساز زاویه مقابل به آن ضلع است. که این عمود منصف (یا نیمساز) محور تقارن آن چند ضلعی است
متوازی الاضلاع
چهار ضلعی است که هر دو ضلع آن موازی باشند. در متوازی الاضلاع، فاصله هر دو ضلع مقابل به هم را ارتفاع می نامند.

الف) در هر متوازی الاضلاع، اضلاع مقابل با هم برابر هستند.

ب)درهر متوازی الاضلاع زاویه های مقابل برابرند و هر دو زاویه مجاور یک ضلع مکمل یکدیگرند. همچنین مجموع دو زاویه مجاور برابر 180 درجه است.

ج) در هر متوازی الاضلاع قطرها منصف یکدیگرند.

د) در هر متوازی الاضلاع نقطه تقاطع دو قطر مرکز تقارن آن شکل است.

ه‍) مساحت متوازی الاضلاع برابر با حاصلضرب قاعده در ارتفاع وارد بر آن است.

ز) در هر متوازی الاضلاع، نیمسازهای داخلی دو به دو بر هم عمودند.

لوزی

لوزی متوازی الاضلاعی است که چهار ضلع آن با هم برابر باشند. بنابراین لوزی کلیه ویژگیهای متوازی الاضلاع را دارد.

مساحت و محیط لوزی :
مساحت لوزی برابر نصف حاصلضرب اندازه های دو قطر است.

نکته 1 :
از هر لوزی یک دایره محاطی می گذرد.
کایت یا شبه لوزی ، چهار ضلعی محدبی است که دارای دو جفت اضلاع مجاور مساوی با دو اندازه مختلف باشد. در واقع کایت چهار ضلعی محدبی است که دارای دو قطر عمود بر هم باشد و فقط یکی از قطرها منصف قطر دیگر باشد. قطری که منصف قطر دیگر است، محور تقارن کایت و همچنین نیمساز دو زاویه مقابل است. مساحت کایت مانند مساحت لوزی محاسبه می شود.
مستطیل
مستطیل متوازی الاضلاعی است که یک زاویه آن قائمه باشد. بنابراین مستطیل کلیه ویژگیهای متوازی الاضلاع را داراست. خطی که وسط دو ضلع مقابل را به هم وصل کند محور تقارن مستطیل است. بنابراین مستطیل دو محور تقارن دارد.

نکته 1 :
مساحت مستطیل برابر حاصلضرب طول در عرض آن است.

نکته 2 :
بر مستطیل یک دایره محیطی می گذرد.
مربع

مربع مستطیلی است که چهار ضلع آن با هم مساوی باشد و یا می توان گفت ، مربع لوزی است که یک زاویه آن قائمه باشد. بنابراین مربع کلیه ویژگیهای متوازی الاضلاع، مستطیل و لوزی را دارد.

نکته 1 :
در هر مربع قطرها بر هم عمود و با هم برابر و هر کدام محور تقارن شکل هستند.

نکته 2 :
مربع چهار محور تقارن (به تعداد اضلاع) دارد. مربع یک چهار ضلعی منتظم است و کلید ویژگیهای چند ضلعی منتظم را داراست.
مساحت و محیط مربع : مساحت مربع برابر مجذوب یک ضلع است.

ذوزنقه

هر چهار ضلعی که فقط دو ضلع آن با هم موازی باشند، ذوزنقه نامیده می شود. دو ضلع موازی را قاعده ها، و دو ضلع غیرموازی را ساقها می نامند. اگر دو ساق ذوزنقه با هم مساوی باشند ذوزنقه را متساوی الساقین می نامند، اگر یکی از ساقها بر دو قاعده عمود باشد ذوزنقه را قائم الزاویه می نامند.

نکته 1 :
در هر ذوزنقه دو زاویه مجاوز بر هر ساق مکمل یکدیگرند.

نکته 2 :
در هر ذوزنقه متساوی الساقین دو قطر با هم و همچنین دو زاویه مجاور به هر قاعده با هم برابر هستند.

نکته 3 :
پاره خطی که دو سر آن وسط های دو ساق ذوزنقه باشد، موازی دو قاعده آن ذوزنقه و اندازه آن برابر نصف مجموع اندازه های دو قاعده ذوزنقه است.

مساحت ذوزنقه :
مساحت ذوزنقه با نصف حاصلضرب مجموع دو قاعده درارتفاع آن برابر است.
چهار ضلعی های محیطی
چهار ضلعی محیطی چهار ضلعی است که اضلاع آن بر یک دایره مماس باشند.

نکته 1 :
درهر چهار ضلعی محیطی مجموع دو ضلع مقابل با مجموع دو ضلع مقابل دیگر برابر است.


چهارضلعی های محاطی
چهار ضلعی محاطی چهار ضلعی است که رأسهای آن بر یک دایره واقع باشد.

نکته 1 :
در هر چهار ضلعی محاطی مجموع دو زاویه مقابل 180 درجه است.