پرسش های چهارگزینه ای فصل اول ریاضی ۷

پرسش های چهارگزینه ای فصل اول ریاضی ۷ به همراه پاسخ تشرحی

کتاب پرسش های چهارگزینه ای ریاضیات ۷  ویژه استفاده دانش آموزان ممتاز و علاقه مند به ریاضی تالیف گردیده است.

هر فصل این کتاب در چهار بخش به شرح زیر می باشد:
بخش اول : آموزش خلاصه ی مباحث و نکات مهم به همراه سوالات تستی آسان
بخش دوم : سوالات تستی سطح متوسط
بخش سوم : سوالات تستی سطح سخت
بخش چهارم : پیش به سوی مسابقات جهانی.

در ادامه ی مطلب می توانید فصل اول این کتاب که شامل خلاصه درس و ۱۱۰ سوال تستی (ساده – متوسط – سخت) و ۶۹ سوال تستی از سوالات مسابقات جهانی ریاضی (روبوکاپ، کانگورو، المپیاد، IMC و…) به همراه پاسخ تشریحی می باشد را دانلود نمایید

از اینجا دانلود کنید            فایل فشرده است پس از دانلود با WINRAR از حالت فشرده خارج کنید
رمز::: WWW.riazisara.ir

جدول سحرآمیز بنیامین فرانکلین

جدول سحرآمیز بنیامین فرانکلین

 

بنیامین فرانکلین (Benjamin Franklin) در سال ۱۷۰۶ میلادی در بوستون، ماساچوست آمریکا به دنیا آمد. او یک دیپلمات، دانشمند، سیاستمدار و صاحب چاپخانه بود. شهرت او بیشتر به دلیل کارهایی است که در زمینه برق انجام داد و برقگیر را اختراع کرد. فرانکلین در سال ۱۷۹۰ درگذشت. او هرگز تا پایان عمر ۸۴ ساله اش دست از پژوهش در زمینه های علمی بر نداشت و به دنبال کشف یا اختراع بود. یکی از سرگرمی های این دانشمند بزرگ طرح جدول های سحرآمیز ریاضی بود. جدولی که در زیر مشاهده می شود یکی از جدول های سحرآمیز اوست. فرانکلین برای طرح این جدول از عدد های پی در پی ۱ تا ۶۴ استفاده کرده است:

 

۴۵	۳۶	۲۹	۲۰	۱۳	۴	۶۱	۵۲
۱۹	۳۰	۳۵	۴۶	۵۱	۶۲	۳	۱۴
۴۴	۳۷	۲۸	۲۱	۱۲	۵	۶۰	۵۳
۲۲	۲۷	۳۸	۴۳	۵۴	۵۹	۶	۱۱
۴۲	۳۹	۲۶	۲۳	۱۰	۷	۵۸	۵۵
۲۴	۲۵	۴۰	۴۱	۵۶	۵۷	۸	۹
۴۷	۳۴	۳۱	۱۸	۱۵	۲	۶۳	۵۰
۱۷	۳۲	۳۳	۴۸	۴۹	۶۴	۱	۱۶

از شگفتی های این جدول سحرآمیز این است که حاصل جمع هشت عدد هر ردیف افقی یا هر ستون عمودی ۲۶۰ است. تفاوت جدول فرانکلین با جدول های سحرآمیز دیگر در این است که حاصل جمع اعداد هر یک از قطر های آن برابر با حاصل جمع هر ردیف یا هر ستون جدول نیست ولی این جدول شگفتی های دیگری داد که آن را بسیار سحر آمیز کرده است.

حاصل جمع هر مستطیل ۴*۲ و ۲*۴ دلخواه برابر ۲۶۰ است.

حاصل جمع اعداد درون هر دو مربع ۲*۲ دلخواه برابر ۲۶۰ است.

اگر اعداد درون مربع ۲*۲ موجود در ستون وسطی را با دو مستطیل ۱*۲ موجود در همان ردیف با یک ستون فاصله از طرفین با هم جمع کنیم حاصل باز هم ۲۶۰ خواهد بود . این قاعده به صورت عمودی نیز برقرار است.

به نظر می رسد حالات مشابه دیگری هم وجود داشته باشد که با بررسی و تفحص بیشتر می توان به آنها دست یافت.

آیا شما می توانید روابط دیگری در این جدول پیدا کنید؟

در پایان این پست، سخنی از مبتکر این جدول سحرآمیز را برای شما درج می کنیم:

«اگر می خواهی پس از مرگ فراموش نشوی، یا چیزی بنویس که قابل خواندن باشد یا کاری کن که قابل نوشتن باشد.»

جدول سحرآمیز بنیامین فرانکلین

جدول سحرآمیز بنیامین فرانکلین

 

بنیامین فرانکلین (Benjamin Franklin) در سال ۱۷۰۶ میلادی در بوستون، ماساچوست آمریکا به دنیا آمد. او یک دیپلمات، دانشمند، سیاستمدار و صاحب چاپخانه بود. شهرت او بیشتر به دلیل کارهایی است که در زمینه برق انجام داد و برقگیر را اختراع کرد. فرانکلین در سال ۱۷۹۰ درگذشت. او هرگز تا پایان عمر ۸۴ ساله اش دست از پژوهش در زمینه های علمی بر نداشت و به دنبال کشف یا اختراع بود. یکی از سرگرمی های این دانشمند بزرگ طرح جدول های سحرآمیز ریاضی بود. جدولی که در زیر مشاهده می شود یکی از جدول های سحرآمیز اوست. فرانکلین برای طرح این جدول از عدد های پی در پی ۱ تا ۶۴ استفاده کرده است:

 

۴۵	۳۶	۲۹	۲۰	۱۳	۴	۶۱	۵۲
۱۹	۳۰	۳۵	۴۶	۵۱	۶۲	۳	۱۴
۴۴	۳۷	۲۸	۲۱	۱۲	۵	۶۰	۵۳
۲۲	۲۷	۳۸	۴۳	۵۴	۵۹	۶	۱۱
۴۲	۳۹	۲۶	۲۳	۱۰	۷	۵۸	۵۵
۲۴	۲۵	۴۰	۴۱	۵۶	۵۷	۸	۹
۴۷	۳۴	۳۱	۱۸	۱۵	۲	۶۳	۵۰
۱۷	۳۲	۳۳	۴۸	۴۹	۶۴	۱	۱۶

از شگفتی های این جدول سحرآمیز این است که حاصل جمع هشت عدد هر ردیف افقی یا هر ستون عمودی ۲۶۰ است. تفاوت جدول فرانکلین با جدول های سحرآمیز دیگر در این است که حاصل جمع اعداد هر یک از قطر های آن برابر با حاصل جمع هر ردیف یا هر ستون جدول نیست ولی این جدول شگفتی های دیگری داد که آن را بسیار سحر آمیز کرده است.

حاصل جمع هر مستطیل ۴*۲ و ۲*۴ دلخواه برابر ۲۶۰ است.

حاصل جمع اعداد درون هر دو مربع ۲*۲ دلخواه برابر ۲۶۰ است.

اگر اعداد درون مربع ۲*۲ موجود در ستون وسطی را با دو مستطیل ۱*۲ موجود در همان ردیف با یک ستون فاصله از طرفین با هم جمع کنیم حاصل باز هم ۲۶۰ خواهد بود . این قاعده به صورت عمودی نیز برقرار است.

به نظر می رسد حالات مشابه دیگری هم وجود داشته باشد که با بررسی و تفحص بیشتر می توان به آنها دست یافت.

آیا شما می توانید روابط دیگری در این جدول پیدا کنید؟

در پایان این پست، سخنی از مبتکر این جدول سحرآمیز را برای شما درج می کنیم:

«اگر می خواهی پس از مرگ فراموش نشوی، یا چیزی بنویس که قابل خواندن باشد یا کاری کن که قابل نوشتن باشد.»

مثلث خیام ـ پاسکال، مثلث همه کاره

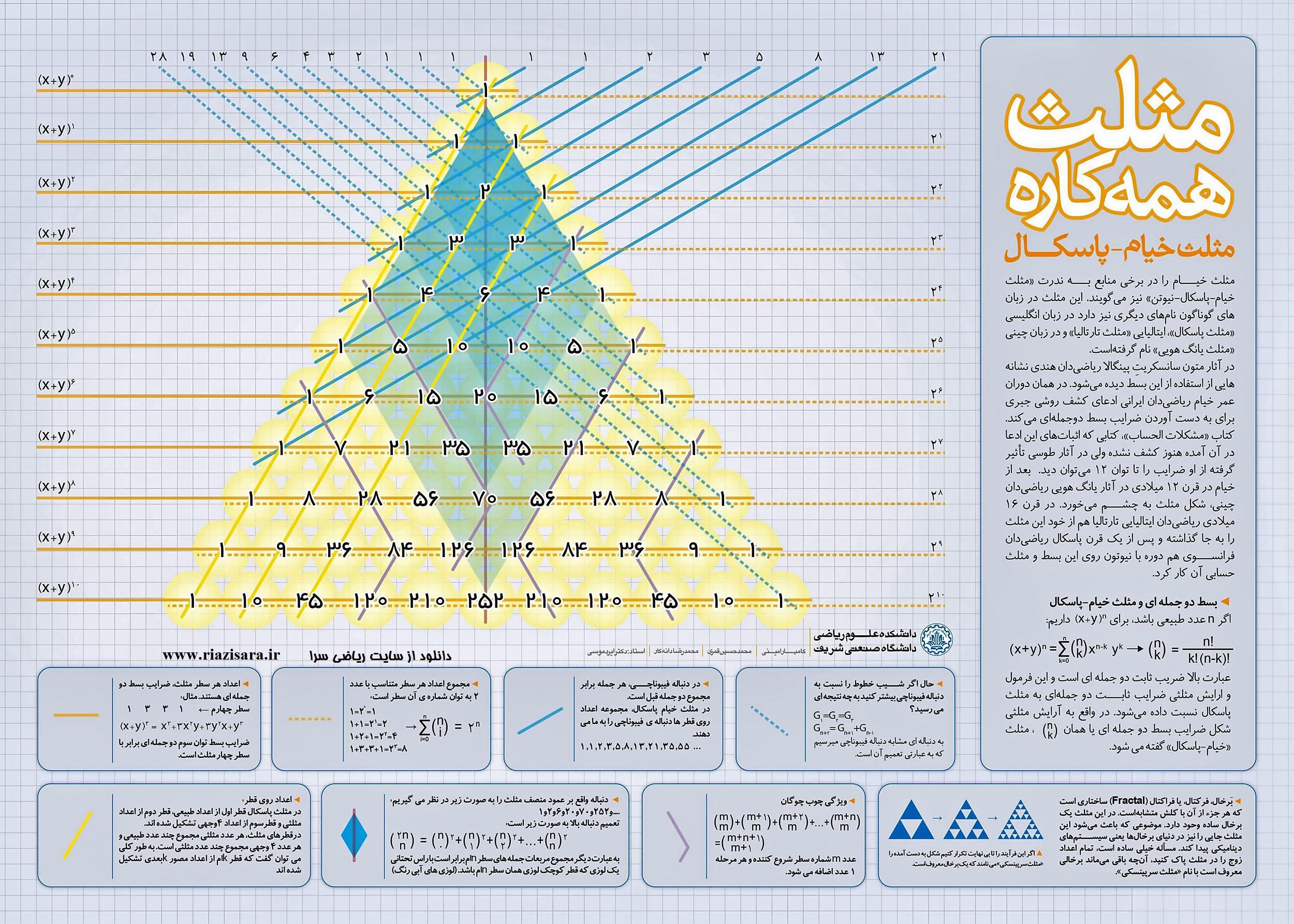
مثلث خیام را در برخی منابع به ندرت «مثلث خیام – پاسکال – نیوتن» نیز می گویند. این مثلث در زبان های گوناگون نام های دیگری نیز دارد. در زبان انگلیسی «مثلث پاسکال»، در زبان ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته است.

در آثار متون سانسکریت پینگالا ریاضی دان هندی نشانه هایی از استفاده از این بسط دیده می شود. در همان دوران عمر خیام ریاضی دان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجمله ای می کند. کتاب «مشکلات الحساب»، کتابی که اثبات های این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تاثیر گرفته از او ضرایب را تا توان ۱۲ می توان دید. بعد از خیام در قرن ۱۲ میلادی در آثار یانگ هویی ریاضی دان چینی، شکل مثلث به چشم می خورد. در قرن ۱۶ میلادی ریاضی دان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضی دان فرانسوی هم دوره با نیوتن روی این بسط و مثلث حسابی آن کار کرد.

خلق تصاویر زیبای ریاضی

تصاویر ریاضی

ارتباط بین ریاضیات و هنر به هزاران سال پیش برمی‌گردد، ریاضیات بکار رفته در طراحی کلیساهای گوتیک Gothic، پنجره رز، فرش شرقی، موزاییک و کاشی کاری‌ها. اشکال هندسی، اساس طرح‌های کوبیسم و بسیاری از تجلی‌های انتزاعی بوده و مجسمه سازان برنده جوایز، توپولوژی را به عنوان پایه‌ای اساسی در قطعه خود استفاده کرده‌اند. در آثار هنری هنرمند هلندی M.C. اشر Escher، مفاهیمی شامل نهایت، باند موبیوس، کاشیکاری، تغییر شکل، بازتاب، مواد افلاطونی، مارپیچ، تقارن و صفحه هایپربولیک وجود دارد.
همچنان ریاضیدانان و هنرمندان به خلق آثار خیره کننده در تمام رسانه‌ها و کشف تجسم ریاضیات – اریگامی، تصاویر کامپیوتری، کاشیکاری، فرکتال، هنر آنامورفیک و … ادامه می‌دهند.

مفاهیم ریاضی نشان داده شده در قالب تصاویر، کاری از حمید نادری یگانه را در ادامه ببینید.

---

تصویر فوق شامل ۱۰۰۰ قطعه خط است. برای هر I = 1،۲،۳، …، ۱۰۰۰ نقاط پایانی قطعهi ام است:

(-sin(2πi/1000), -cos(2πi/1000)) and ((-1/2)sin(8πi/1000), (-1/2)cos(12πi/1000))

---

تصویر فوق شامل ۱۰۰۰ قطعه خط است. برای هر I = 1،۲،۳، …، ۱۰۰۰ نقاط پایانی قطعهi ام است:

(-sin(4πi/1000), -cos(2πi/1000)) and ((-1/2)sin(8πi/1000), (-1/2)cos(4πi/1000))

---

تصویر فوق شامل ۱۰۰۰ قطعه خط است. برای هر I = 1،۲،۳، …، ۱۰۰۰ نقاط پایانی قطعهi ام است:

(-sin(8πi/1000), -cos(2πi/1000)) and ((-1/2)sin(6πi/1000), (-1/2)cos(2πi/1000